'접근', '역량', '활용' 을 유형화의 변수로 활용하여 K-means 클러스터링을 수행했다. 클러스터 수는 엘보우 메소드(Elbow Method)를 통해 설정하였고, 'k-means++' 방법으로 초기 클러스터 중심을 설정, 최대 반복 횟수(max_iter)와 랜덤 시드(random_state)도 설정해서 클러스터링 해줬다.

결과

T-SNE를 사용한 시각화 : t-SNE를 사용하여 차원 축소 후 시각화

소스코드는 다음과 같다.

import matplotlib
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# read data xlsx
df = pd.read_excel('data.xlsx')

# read the columns from xlsx
#df2 = pd.read_excel("codebook.xlsx")
from matplotlib import rc
rc('font', family='AppleGothic')
every_df = pd.read_csv('every_data.csv')
plt.rcParams['axes.unicode_minus'] = False
# only keep the columns we need which is 변수정보, Unnamed: 1,  Unnamed: 2
# df2 = df2[['변수 정보', 'Unnamed: 1', 'Unnamed: 2']]
# # drop the first row
# df2 = df2.drop(df2.index[0])
# # drop the last row
# df2 = df2.drop(df2.index[-1])

# mapping the columns name which is on df2 to df using key '변수 정보' and value 'Unnamed: 2'
# and rename the columns name
#df = df.rename(columns=dict(zip(df2['변수 정보'], df2['Unnamed: 2'])))
print()
# unify the columns name Q2A11, Q2A12, Q2A13
# if value is overlap, then keep the highest value
every_df['Q2A1'] = every_df[['Q2A11', 'Q2A12', 'Q2A13']].max(axis=1)
df['Q2A1'] = df[['Q2A11', 'Q2A12', 'Q2A13']].max(axis=1)
# drop the columns Q2A11, Q2A12, Q2A13
every_df = every_df.drop(['Q2A11', 'Q2A12', 'Q2A13'], axis=1)
df = df.drop(['Q2A11', 'Q2A12', 'Q2A13'], axis=1)
# do Normalization on every comlumns except ID
# min_val = every_df.iloc[:, 1:].min()
# max_val = every_df.iloc[:, 1:].max()
# every_df.iloc[:, 1:] = (every_df.iloc[:, 1:] - min_val) / (max_val - min_val)
#
# df.iloc[:, 1:] = (df.iloc[:, 1:] - min_val) / (max_val - min_val)
"""
['ID', 'Q1A1', 'Q1A2', 'Q2A2', 'Q2A3', 'Q3', 'Q4A1', 'Q4A2', 'Q4A3', 'Q4A4', 'Q4A5', 'Q4A6', 'Q4A7', 'Q5A1', 'Q5A2', 'Q5A3', 'Q5A4', 'Q5A5', 'Q5A6', 'Q5A7', 'Q6', 'Q7A1', 'Q7A2', 'Q7A3', 'Q8A1', 'Q8A2', 'Q8A3', 'Q8A4', 'Q8B1', 'Q8B2', 'Q8B3', 'Q8B4', 'Q9A1', 'Q9A2', 'Q9A3', 'Q9A4', 'Q9A5', 'Q9B1', 'Q9B2', 'Q9B3', 'Q9B4', 'Q9B5', 'Q10A1', 'Q10A2', 'Q10A3', 'Q10A4', 'Q10B1', 'Q10B2', 'Q10B3', 'Q10B4', 'Q11A1', 'Q11A2', 'Q11B1', 'Q11B2', 'Q12A1', 'Q12A2', 'Q12B1', 'Q12B2', 'Q13A1', 'Q13A2', 'Q13A3', 'Q13A4', 'Q13B1', 'Q13B2', 'Q13B3', 'Q13B4', 'Q14A1', 'Q14A2', 'Q14A3', 'Q14A4', 'Q14B1', 'Q14B2', 'Q14B3', 'Q14B4', 'Q15A1', 'Q15A2', 'Q15A3', 'Q15A4', 'Q15A5', 'Q15A6', 'Q16A01', 'Q16A02', 'Q16A03', 'Q16A04', 'Q16A05', 'Q16A06', 'Q16A07', 'Q16A08', 'Q16A09', 'Q16A10', 'Q17A1', 'Q17A2', 'Q17A3', 'Q17A4', 'Q18A1', 'Q18A2', 'Q18A3', 'Q18A4', 'Q19A1', 'Q19A2', 'Q19A3', 'Q19A4', 'Q19A5', 'Q19A6', 'Q19A7', 'Q19A8', 'Q20A1', 'Q20A2', 'Q20A3', 'Q20A4', 'Q20A5', 'Q21AA1', 'Q21AA2', 'Q21AA3', 'Q21AA4', 'Q21AA5', 'Q21AA6', 'Q21AA7', 'Q21AA8', 'Q21BA1', 'Q21BA2', 'Q21BA3', 'Q21BA4', 'Q21BB1', 'Q21BB2', 'Q21BB3', 'Q21BB4', 'Q21BC1', 'Q21BC2', 'Q21BC3', 'Q21BC4', 'Q21BCA11', 'Q21BCA12', 'Q21BCA21', 'Q21BCA22', 'Q21BCA31', 'Q21BCA32', 'Q21BCA41', 'Q21BCA42', 'Q21CA1', 'Q21CA2', 'Q21CA3', 'Q21CA4', 'Q21CA5', 'Q21CA6', 'Q21CB1', 'Q21CB2', 'Q21CB3', 'Q21CB4', 'Q21CC1', 'Q21CC2', 'Q21CC3', 'Q21CC4', 'Q22A01', 'Q22A02', 'Q22A03', 'Q22A04', 'Q22A05', 'Q22A06', 'Q22A07', 'Q22A08', 'Q22A09', 'Q22A10', 'Q22A11', 'Q22A12', 'Q22A13', 'Q22A14', 'Q22A15', 'Q22A16', 'Q22A17', 'Q22A18', 'Q22A19', 'Q22A20', 'Q22A21', 'Q22A22', 'Q22A23', 'Q22A24', 'Q22A25', 'Q22A26', 'Q22A27', 'Q22A28', 'Q23', 'Q24A1', 'Q24A2', 'Q24A3', 'Q24A4', 'Q25', 'Q26', 'Q27', 'Q28A01', 'Q28A02', 'Q28A03', 'Q28A04', 'Q28A05', 'Q28A06', 'Q28A07', 'Q28A08', 'Q28A09', 'Q28A10', 'Q28A11', 'Q28A12', 'Q29A1', 'Q29A2', 'Q29A3', 'Q29A4', 'Q29A5', 'Q29A6', 'Q29A7', 'ADQ1', 'ADQ2', 'ADQ3', 'ADQ3A', 'ADQ4', 'ADQ5', 'ADQ6', 'ADQ7', 'ADQ8', 'ADQ8A', 'ADQ8A1', 'ADQ8A2', 'ADQ8A3', 'ADQ8A4', 'ADQ8A5', 'ADQ8A6', 'ADQ8A7', 'ADQ8A8', 'ADQ9', 'ADQ101', 'ADQ102', 'ADQ103', 'WT2', 'Q2A1']
"""
# 접근: Q1-3 +Q6-7(12문항)
# sum value of column name 'Q1A1', 'Q1A2', 'Q2A2', 'Q2A3', 'Q3'
every_df['Q1-3'] = every_df[['Q1A1', 'Q1A2', 'Q2A2', 'Q2A3', 'Q3']].sum(axis=1)
df['Q1-3'] = df[['Q1A1', 'Q1A2', 'Q2A2', 'Q2A3', 'Q3']].sum(axis=1)
# sum value of column name 'Q6', 'Q7A1', 'Q7A2', 'Q7A3'
every_df['Q6-7'] = every_df[['Q6', 'Q7A1', 'Q7A2', 'Q7A3']].sum(axis=1)
df['Q6-7'] = df[['Q6', 'Q7A1', 'Q7A2', 'Q7A3']].sum(axis=1)
# sum the value of df columns name 'Q1-3', 'Q6-7' to variable
every_df['접근'] = every_df[['Q1-3', 'Q6-7']].sum(axis=1)
df['접근'] = df[['Q1-3', 'Q6-7']].sum(axis=1)


#역량은 Q4 + Q5 (14문항)
# sum value of column name 'Q4A1', 'Q4A2', 'Q4A3', 'Q4A4', 'Q4A5', 'Q4A6', 'Q4A7'
every_df['Q4'] = every_df[['Q4A1', 'Q4A2', 'Q4A3', 'Q4A4', 'Q4A5', 'Q4A6', 'Q4A7']].sum(axis=1)
df['Q4'] = df[['Q4A1', 'Q4A2', 'Q4A3', 'Q4A4', 'Q4A5', 'Q4A6', 'Q4A7']].sum(axis=1)
# sum value of column name 'Q5A1', 'Q5A2', 'Q5A3', 'Q5A4', 'Q5A5', 'Q5A6', 'Q5A7'
every_df['Q5'] = every_df[['Q5A1', 'Q5A2', 'Q5A3', 'Q5A4', 'Q5A5', 'Q5A6', 'Q5A7']].sum(axis=1)
df['Q5'] = df[['Q5A1', 'Q5A2', 'Q5A3', 'Q5A4', 'Q5A5', 'Q5A6', 'Q5A7']].sum(axis=1)
# sum the value of df columns name 'Q4', 'Q5' to variable
every_df['역량'] = every_df[['Q4', 'Q5']].sum(axis=1)
df['역량'] = df[['Q4', 'Q5']].sum(axis=1)

# 활용은 Q8-Q14+Q28-29(69문항)
# sum value of column name 'Q8A1', 'Q8A2', 'Q8A3', 'Q8A4', 'Q8B1', 'Q8B2', 'Q8B3', 'Q8B4'
every_df['Q8'] = every_df[['Q8A1', 'Q8A2', 'Q8A3', 'Q8A4', 'Q8B1', 'Q8B2', 'Q8B3', 'Q8B4']].sum(axis=1)
df['Q8'] = df[['Q8A1', 'Q8A2', 'Q8A3', 'Q8A4', 'Q8B1', 'Q8B2', 'Q8B3', 'Q8B4']].sum(axis=1)
# sum value of column name 'Q9A1', 'Q9A2', 'Q9A3', 'Q9A4', 'Q9A5', 'Q9B1', 'Q9B2', 'Q9B3', 'Q9B4', 'Q9B5'
every_df['Q9'] = every_df[['Q9A1', 'Q9A2', 'Q9A3', 'Q9A4', 'Q9A5', 'Q9B1', 'Q9B2', 'Q9B3', 'Q9B4', 'Q9B5']].sum(axis=1)
df['Q9'] = df[['Q9A1', 'Q9A2', 'Q9A3', 'Q9A4', 'Q9A5', 'Q9B1', 'Q9B2', 'Q9B3', 'Q9B4', 'Q9B5']].sum(axis=1)
# sum value of column name 'Q10A1', 'Q10A2', 'Q10A3', 'Q10A4', 'Q10B1', 'Q10B2', 'Q10B3', 'Q10B4'
every_df['Q10'] = every_df[['Q10A1', 'Q10A2', 'Q10A3', 'Q10A4', 'Q10B1', 'Q10B2', 'Q10B3', 'Q10B4']].sum(axis=1)
df['Q10'] = df[['Q10A1', 'Q10A2', 'Q10A3', 'Q10A4', 'Q10B1', 'Q10B2', 'Q10B3', 'Q10B4']].sum(axis=1)
# sum value of column name 'Q11A1', 'Q11A2', 'Q11B1', 'Q11B2'
every_df['Q11'] = every_df[['Q11A1', 'Q11A2', 'Q11B1', 'Q11B2']].sum(axis=1)
df['Q11'] = df[['Q11A1', 'Q11A2', 'Q11B1', 'Q11B2']].sum(axis=1)
# sum value of column name 'Q12A1', 'Q12A2', 'Q12B1', 'Q12B2'
every_df['Q12'] = every_df[['Q12A1', 'Q12A2', 'Q12B1', 'Q12B2']].sum(axis=1)
df['Q12'] = df[['Q12A1', 'Q12A2', 'Q12B1', 'Q12B2']].sum(axis=1)
# sum value of column name 'Q13A1', 'Q13A2', 'Q13A3', 'Q13A4', 'Q13B1', 'Q13B2', 'Q13B3', 'Q13B4'
every_df['Q13'] = every_df[['Q13A1', 'Q13A2', 'Q13A3', 'Q13A4', 'Q13B1', 'Q13B2', 'Q13B3', 'Q13B4']].sum(axis=1)
df['Q13'] = df[['Q13A1', 'Q13A2', 'Q13A3', 'Q13A4', 'Q13B1', 'Q13B2', 'Q13B3', 'Q13B4']].sum(axis=1)
# sum value of column name 'Q14A1', 'Q14A2', 'Q14A3', 'Q14A4', 'Q14B1', 'Q14B2', 'Q14B3', 'Q14B4'
every_df['Q14'] = every_df[['Q14A1', 'Q14A2', 'Q14A3', 'Q14A4', 'Q14B1', 'Q14B2', 'Q14B3', 'Q14B4']].sum(axis=1)
df['Q14'] = df[['Q14A1', 'Q14A2', 'Q14A3', 'Q14A4', 'Q14B1', 'Q14B2', 'Q14B3', 'Q14B4']].sum(axis=1)
# sum value of column name 'Q28A01', 'Q28A02', 'Q28A03', 'Q28A04', 'Q28A05', 'Q28A06', 'Q28A07', 'Q28A08', 'Q28A09', 'Q28A10', 'Q28A11', 'Q28A12'
every_df['Q28'] = every_df[['Q28A01', 'Q28A02', 'Q28A03', 'Q28A04', 'Q28A05', 'Q28A06', 'Q28A07', 'Q28A08', 'Q28A09', 'Q28A10', 'Q28A11', 'Q28A12']].sum(axis=1)
df['Q28'] = df[['Q28A01', 'Q28A02', 'Q28A03', 'Q28A04', 'Q28A05', 'Q28A06', 'Q28A07', 'Q28A08', 'Q28A09', 'Q28A10', 'Q28A11', 'Q28A12']].sum(axis=1)
# sum value of column name 'Q29A1', 'Q29A2', 'Q29A3', 'Q29A4', 'Q29A5', 'Q29A6', 'Q29A7'
every_df['Q29'] = every_df[['Q29A1', 'Q29A2', 'Q29A3', 'Q29A4', 'Q29A5', 'Q29A6', 'Q29A7']].sum(axis=1)
df['Q29'] = df[['Q29A1', 'Q29A2', 'Q29A3', 'Q29A4', 'Q29A5', 'Q29A6', 'Q29A7']].sum(axis=1)
# sum the value of df columns name 'Q8', 'Q9', 'Q10', 'Q11', 'Q12', 'Q13', 'Q14', 'Q28', 'Q29' to variable
every_df['활용'] = every_df[['Q8', 'Q9', 'Q10', 'Q11', 'Q12', 'Q13', 'Q14', 'Q28', 'Q29']].sum(axis=1)
df['활용'] = df[['Q8', 'Q9', 'Q10', 'Q11', 'Q12', 'Q13', 'Q14', 'Q28', 'Q29']].sum(axis=1)
#종합 지수는 접근 *0.2 + 역량 *0.4 + 활용 *0.4 이구요.
# multiply the value of df columns name '접근', '역량', '활용' to variable


# 접근 역량 활용 항목에 대해서 각각 평균을 내주세요
# calculate the mean value of df columns name '접근', '역량', '활용'
df['접근_mean'] = df[['접근']].mean(axis=1)
df['역량_mean'] = df[['역량']].mean(axis=1)
df['활용_mean'] = df[['활용']].mean(axis=1)
every_df['접근_mean'] = every_df[['접근']].mean(axis=1)
every_df['역량_mean'] = every_df[['역량']].mean(axis=1)
every_df['활용_mean'] = every_df[['활용']].mean(axis=1)

every_df['종합지수'] = every_df[['접근', '역량', '활용']].mul([0.2, 0.4, 0.4]).sum(axis=1)
df['종합지수'] = df[['접근', '역량', '활용']].mul([0.2, 0.4, 0.4]).sum(axis=1)
print()
# do K means through the columns name '접근', '역량', '활용'
# set the number of cluster
num_of_cluster = 3
# set the number of iteration
num_of_iter = 100
# set the initial point of each cluster using df which id is 105820, 103672 and 102611
"""3유형(젤 잘 쓰시는 분) : 105820
2유형(중간유형) : 103672
1유형(디지털소외계층) : 102611"""
#init_point = df[df['ID'].isin([105820, 103672, 102611])][['접근', '역량', '활용']].values

# k means
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=num_of_cluster, init='k-means++', n_init=1, max_iter=num_of_iter, random_state=0).fit(df[['접근', '역량', '활용']])
df['cluster'] = kmeans.labels_

# do visualization using t-sne
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt


# Combine the dataset with the initial points
combined_data = df[['접근', '역량', '활용']]

# Apply t-SNE to reduce the dataset to 2 dimensions for visualization
tsne = TSNE(n_components=2, random_state=0)
tsne_results = tsne.fit_transform(df[['접근', '역량', '활용']])

# Add the t-SNE results as new columns in the DataFrame
df['tsne-2d-one'] = tsne_results[:, 0]
df['tsne-2d-two'] = tsne_results[:, 1]

# Visualize the clusters in the t-SNE transformed space
plt.figure(figsize=(16,10))
sns.scatterplot(
    x="tsne-2d-one", y="tsne-2d-two",
    hue=df['cluster'].astype(str),  # Convert cluster numbers to strings for the color palette
    palette=sns.color_palette("hsv", num_of_cluster),
    data=df,
    legend="full",
    alpha=0.8
)

plt.title('t-SNE Visualization of Clusters')
plt.xlabel('t-SNE Feature 1')
plt.ylabel('t-SNE Feature 2')
plt.legend(title='Cluster')
plt.show()



# Group by 'cluster' and calculate the mean for '종합지수'
cluster_means = df.groupby('cluster')['종합지수'].mean().reset_index()

# Sort the clusters by mean '종합지수'
cluster_means = cluster_means.sort_values('종합지수')

# Assign the type labels based on sorted means
cluster_mapping = {1: 'A', 2: "B", 0:'C'}

# Map the clusters to the type labels
df['yoohyung'] = df['cluster'].map(cluster_mapping)

# Print the result of the mapping

# Plot the clusters on the scatter plot
plt.figure(figsize=(8,6))
sns.scatterplot(
    x='tsne-2d-one', y='tsne-2d-two',
    hue='yoohyung',
    palette=sns.color_palette('hsv', num_of_cluster),
    data=df,
    legend='full',
    alpha=0.7
)
plt.title('t-SNE results with K-means Clusters')
plt.legend()
plt.show()


# Continue from your previous code

# 1. Assign the type labels based on sorted means of '종합지수'
cluster_means = df.groupby('cluster')['종합지수'].mean().sort_values().index
type_labels = {cluster_means[i]: ('A유형' if i == 0 else 'B유형' if i == 1 else 'C유형') for i in range(num_of_cluster)}
df['유형'] = df['cluster'].map(type_labels)

# 2. Calculate the average, minimum, and maximum values for '접근', '역량', and '활용' for each type
# Adjust the groupby method to use a list of column names
stats_df = df.groupby('유형')[['접근', '역량', '활용', '종합지수']].agg(['mean', 'min', 'max']).reset_index()

# Now flatten the multi-index created by the agg function
stats_df.columns = [' '.join(col).strip() for col in stats_df.columns.values]

# Sort the DataFrame based on the type to match the image: A유형, B유형, then C유형
stats_df['sort'] = stats_df['유형'].map({'A유형': 1, 'B유형': 2, 'C유형': 3})
stats_df.sort_values('sort', inplace=True)
stats_df.drop('sort', axis=1, inplace=True)

# Optionally, rename columns to match the format in the image
stats_df.rename(columns=lambda x: x.replace('_', ' '), inplace=True)

# Add 사례수(비율) column
case_counts = df['유형'].value_counts().rename_axis('유형').reset_index(name='사례수')
case_counts['비율'] = (case_counts['사례수'] / df.shape[0]) * 100
case_counts['사례수(비율)'] = case_counts.apply(lambda x: f"{x['사례수']}({x['비율']:.1f}%)", axis=1)

# Merge the 사례수(비율) with the stats_df
stats_df = pd.merge(stats_df, case_counts[['유형', '사례수(비율)']], on='유형')

# draw table and save it

fig, ax = plt.subplots(figsize=(10, 3))
ax.axis('off')
ax.axis('tight')
ax.table(cellText=stats_df.values, colLabels=stats_df.columns, loc='center')
plt.savefig('table.png', dpi=300, bbox_inches='tight')

노인 소비자의 3가지 유형 결과 분석

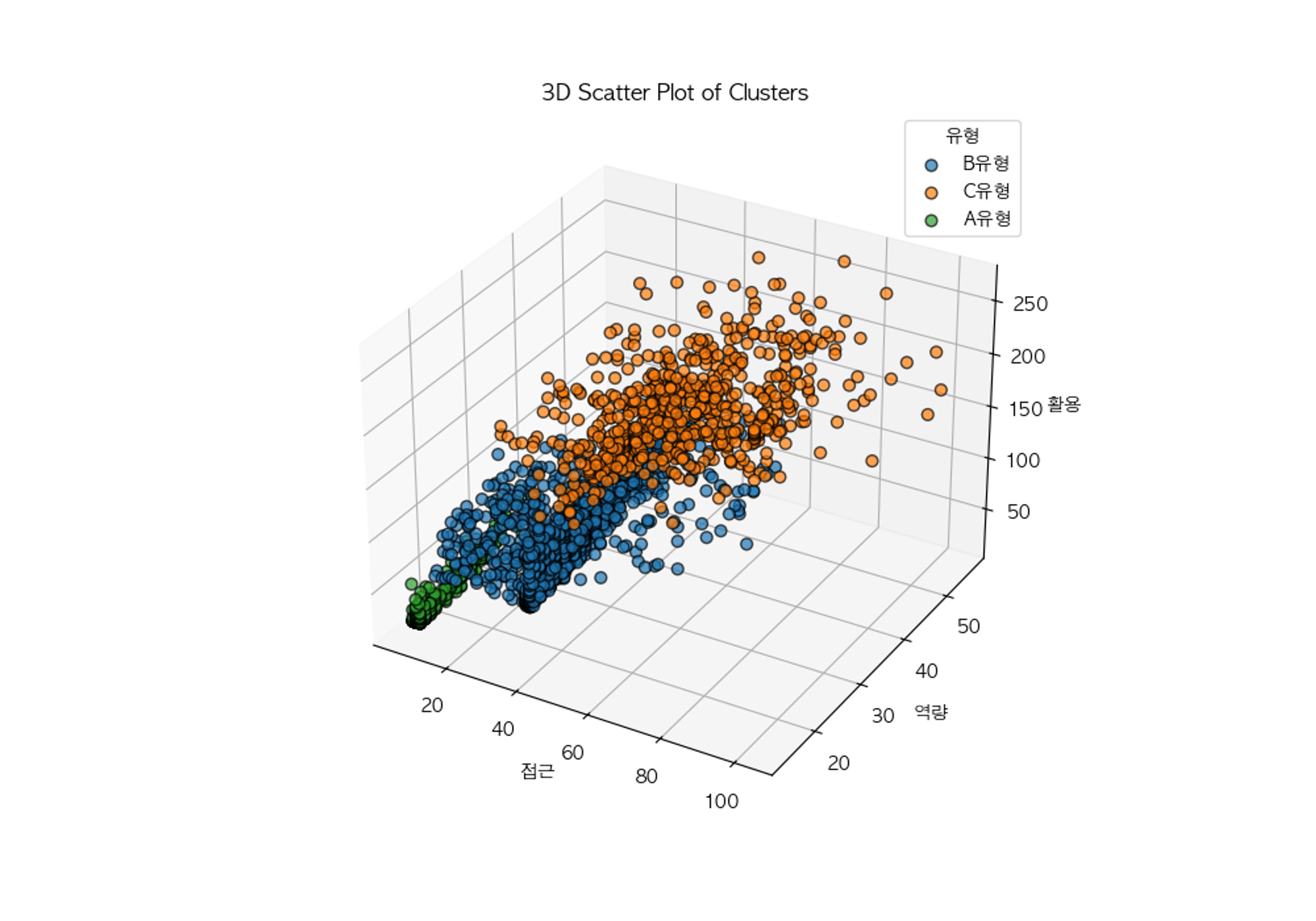
k - means 군집분석 결과, 고령층의 디지털정보화 수준은 크게 3유형으로 분류되었다.

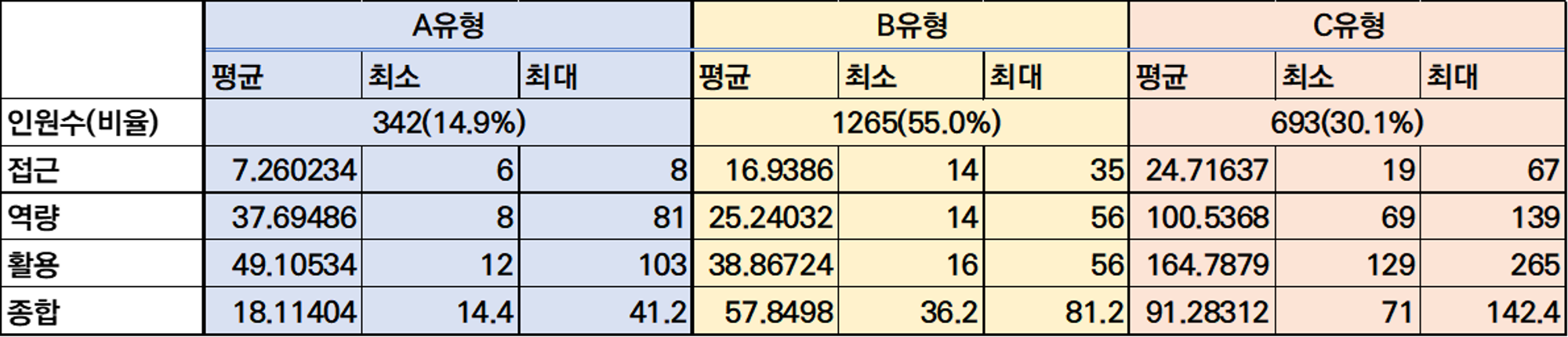
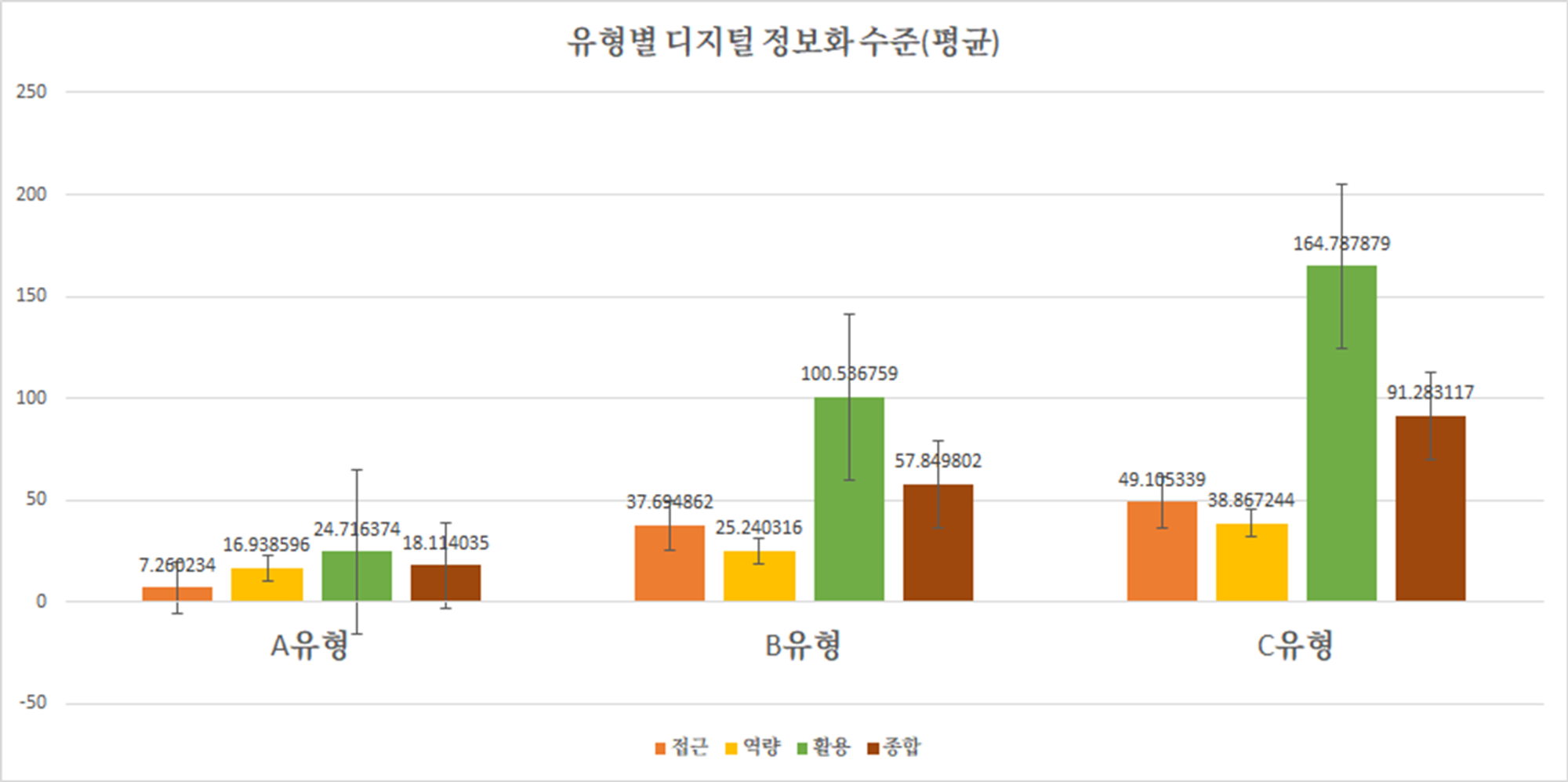
A유형은 전체 고령층 집단의 14.9%로 접근,역량 활용 모든 측면에서 정보화 지수가 확연하게 낮았다. 이 A유형을 ‘시니어 디지털 약자’ 유형으로 정의하겠다.
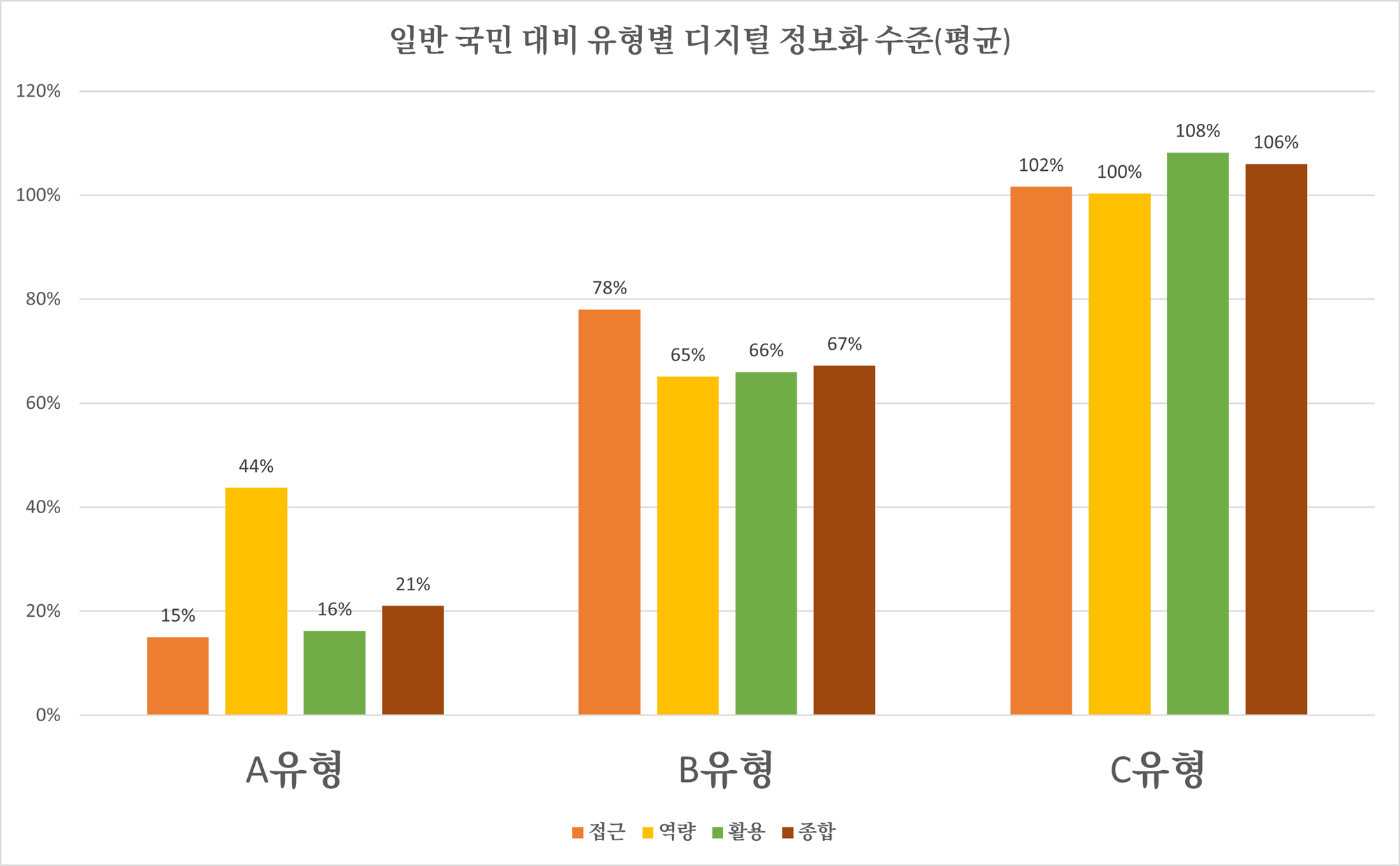
디지털 약자 유형은 ‘디지털 일반 국민과 비교했을 때 일반 국민의 약 20% 정도밖에 활용하지 못하는 수준으로 나타났다. 고령층 집단 내에서도 디지털 취약성이 가장 높은 유형으로 볼 수 있다. 특히, 접근성 지표(15%)가 낮게 나왔는데 이는 pc나 모바일 기기 보유 비율이 낮고, 평소에 인터넷 접속을 거의 하지 않는다고 해석할 수 있다.

이 유형은 디지털 기기 접근성을 높이기 위해 디지털 기기 지원, 무료 와이파이 서비스, 디지털 도우미 파견 등의 직접적인 대면 지원이 필요해 보인다.

B유형은 전체 고령층 집단의 55%로, 전체 고령층 소비자 유형의 반 이상이 이 유형에 해당한다고 볼 수 있다. 이 B유형을 ‘시니어 일반 사용자’ 유형이라 정의하겠다.

‘시니어 일반 사용자’는 종합 지수가 일반 국민의 67% 정도로 산출되었다. 특히 ‘접근’ 지수(78%)가 비교적 높지만 그에 비해 역량(65%)이나 활용(66%)지수가 낮았다. 일상생활에서 디지털 기기를 쉽게 접할 수 있는 환경에 있지만 이를 활용할 수 있는 능력이 낮은 상황인 것이다.

이 유형은 지속적인 ‘정보화 교육’을 통한 역량 향상의 정책이 필요해 보인다.

C유형은 전체 고령층 집단의 30.1%로 고령층 집단 내 접근,역량 활용 지수가 가장 높다. 이 C유형을 ‘시니어 디지털 프랜드’ 유형으로 정의하겠다.

‘시니어 디지털 프랜드’는 종합 지수가 106%으로 일반 국민과 비슷한 유사하거나 일반 국민보다도 조금 더 높은 수준이다. 이는 ‘노년층’이라 해서 하나의 동질적인 ‘디지털 소외계층’으로 판단해서는 안 된다는 점을 시사한다.

이 유형은 고령층 집단 내 가장 이상적인 유형으로 훗날, 디지털 멘토로서의 일자리 창출도 가능한 유형이다.

kmeans를 활용해 나온 유형별 통계량은 다음 차시에서 다루겠다.